Dados

Pretendemos, neste espaço, reunir dados que possam ilustrar os conceitos emitidos nos Capítulos anteriores. Para isso, contamos com a colaboração dos leitores.

Em Limnologia, não basta a coleta e a simples apresentação dos dados. Os métodos estatísticos são essenciais em experimentos que geram respostas com flutuações como, p.ex., a produção de fitoplâncton relacionada ao aporte de fósforo, ou a variação mensal da profundidade de visibilidade do disco de Secchi.

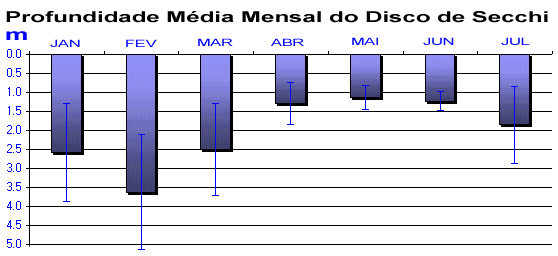
Os gráficos podem, muitas vezes, identificar efeitos (tanto esperados como inusitados) nos dados, mais rapidamente e algumas vezes melhor do que qualquer outro método de análise estatística.

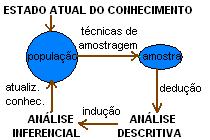
Os métodos clássicos de análise estatística de dados pressupõem as etapas mostradas no croqui ao lado. O primeiro passo é identificar a população-alvo do estudo, que pode ser a água do reservatório. A seguir, há que definir a amostra: tamanho, mensurações, pontos e frequência de coleta, métodos e aparelhos de medida, treinamento da equipe e outras condutas específicas. Os dados resultantes sofrem uma Análise Descritiva e posteriormente, a Análise Inferencial, que possibilita a atualização do conhecimento que se tinha, até o momento, sobre aquele caso específico.

A Amostra

O tamanho da amostra está relacionado ao tema: Suficiência amostral. Se o tamanho da amostra é bastante grande, os resultados das replicações são normalmente distribuídos, ou distribuídos segundo a Curva de Gauss (ou do sino). Assim, para n=>30, a forma da distribuição é "quase" perfeitamente normal.

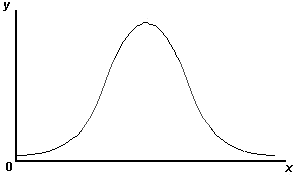
Para a construção da Curva de Gauss (vide croqui ao lado) há que, inicialmente, transformar os dados numa Tabela de Frequência. Para isso, arbitra-se um determinado número de classes e anotam-se quantas vezes os dados da amostra encaixam-se em cada uma. Pode-se estimar em 10 a 15 classes, ou estimá-las pela fórmula de Yule: nc = 2,5 raiz(N)  onde: nc=número de classes e N=número de variáveis.

Em qualquer levantamento, será sempre necessário avaliar se o tamanho da amostra é suficiente para dada precisão requerida. Isto pode ser estimado pela expressão:
n=t2.Sx2/ dms2   onde: n=tamanho da amostra; t=valor tabelado da distribuição  t  de Student para n-1 graus de liberdade; Sx=variância da variável  x  e dms=diferença mínima significativa a ser detectada.

Já a margem de erro na amostra, pode ser estimada pela fórmula:
e = 1 / raiz(n)  onde e=erro esperado e n=número de elementos da amostra.
Assim, numa amostra com 1.600 dados o erro esperado é de 0,025 ou 2,5% enquanto que, noutra com apenas 6, será de 0,408 ou 40,8%.